Calculation of sheet metal bending unfolding size

This paper summarizes the common calculation methods of sheet metal bending unfolding, and analyzes the principles of these common methods by using software combined with calculation. In depth analysis of different materials, different bending angles and different bending radius of sheet metal bending, get the formula to accurately calculate the size of various unfolded materials.

01 Preface

Sheet metal process is usually used to process metal sheet with thickness less than 6 mm. In order to fold the sheet metal parts with high dimensional accuracy, the calculation of unfolding size is very important. The most commonly used sheet metal bending is 90 ° bending, and the inner corner radius of bending is usually equal to the plate thickness.

02 The first calculation method of unfolding material size

The first calculation formula of unfolding size is: unfolding size = the overall size of each side of the bending part and - 1.645 × plate thickness × bending number. Where 1.645 is the bending factor. It is suitable for the calculation of 90 ° bending unfolding size of metal plate under 6 mm (bending inner corner radius is equal to plate thickness). We have verified this formula many times in the actual production. Using different plates, the dimensional tolerance of the folded parts is within a few tenths of a millimeter, which basically meets the demand.

03 The second calculation method of unfolding material size

The second calculation formula of unfolded material size is: unfolded material size = sum of inner dimensions of each side of the bending part + Q × number of bends. Where q is another bending factor. The Q values of different thickness plates are different (see Table 1). When T < 1 mm, q is ignored.

Table 1 comparison table of plate thickness T and bending coefficient Q

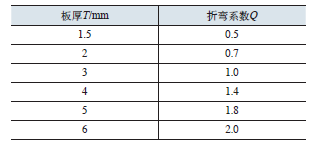
The second calculation method can also be used to calculate the size of 90 ° bending unfolded material of metal plate under 6 mm (the bending inner corner radius is equal to the plate thickness).

04 Calculation example

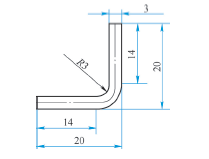
Two methods are used to calculate the unfolded material size of the same bending part shown in Figure 1. The calculation process is as follows.

(1) Method one: unfolding size = 20 + 20-1.645 × 3 × 1 = 40-4.935 = 35.065 (mm).

(2) Method 2: the size of developed material = 17 + 17 + 1 × 1 = 35 (mm).

The calculation results are basically the same. Both methods can be used to calculate 90 ° bending quickly and are widely used in production practice.

05 Using three-dimensional software simulation calculation and analysis

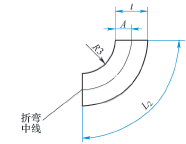
Why can we use these methods to calculate the opening size? Is it possible to more accurately calculate the unfolding size of different materials? We know that in the process of metal sheet bending, plastic deformation will occur at the bending angle. The bending fillet is tensile, and the inner fillet is extrusion. This makes there is a layer in the thickness direction of the sheet, which is neither extruded nor stretched in the bending process. The size after bending is the same as the unfolded size. This layer is called neutral layer. Cut a section in the thickness direction of the bending sheet metal, and a line with constant length in the section is called the bending center line, as shown in Figure 2. The position of this bending line is expressed by K and Y factors, k = A / T, y = k π / 2. The K and Y values of different materials are different, and the size of developed material is also different. The hardness of the material is small, such as brass, y = 0.55, k = 0.35; the hardness is general, such as aluminum, y = 0.64, k = 0.41; the hardness is higher, such as cold rolled steel, spring steel, y = 0.71, k = 0.45. Nowadays many 3D software have sheet metal drawing function, here we use Creo software to simulate sheet metal bending. Creo software also has k and Y settings, by changing their size, you can simulate different bending, so as to calculate or measure the size of the developed material.

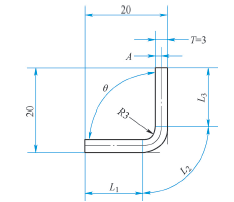
1) Combined with 3D software and K, y value setting, the sheet metal bending is analyzed, as shown in Figure 3. It can be seen from Figure 3 that extrusion and tensile deformation occur in the bending part of the plate during the bending process. When θ = 90 °, L 2 is 1 / 4 arc length. The size of developed material l = l 1 + L 2 + L 3. Among them, L1 = 20-t-r = 14 (mm); L3 = 20-t-r = 14 (mm); L2 = (R + a) π / 2, r = t, so L2 = (T + a) π / 2. Then l = l 1 + (T + a) π / 2 + L 3. Assuming that a = 1.5, that is, k = 0.5, the developed material size L = 14 + (3 + 1.5) π / 2 + 14 = 35.065 (mm) can be calculated.

2) Use the above methods 1 and 2 to calculate the size of unfolded material in Fig. 3. Method 1: l = 20 + 20-1.645 × 3 × 1 = 40-4.935 = 35.065 (mm); method 2: l = 17 + 17 + 1 × 1 = 35 (mm).

It can be seen that method 1 and method 2 are the developed material size calculated when k is set to 0.5. Because the K value of all kinds of metal materials fluctuates around 0.5, and the dimensional tolerance of most sheet metal parts is not high, so setting K to 0.5 can basically calculate the unfolding size of most sheet metal. In order to calculate the unfolding size of right angle bending more accurately, it is necessary to bring the K value of the corresponding material into the formula, so that the folded sheet metal parts have higher dimensional accuracy and smaller tolerance.

06 Calculation method of non right angle bending

What we have been discussing is right angle bending, and the inner corner radius of bending is equal to the plate thickness. Can the bending angle not 90 ° and the inner corner radius ≠ the plate thickness be calculated? Referring to Fig. 3, if the internal angle R ≠ plate thickness, θ ≠ 90 °, then L2 = (R + a) π / 2 = R π / 2 + a π / 2 = R π / 2 + a π T / (2t) = R π / 2 + K π T / 2 = (R π / 2 + YT) θ / 90.

The relationship between the length of the bending part and y, θ is obtained. According to the K, Y values of different materials, the size of the bending part L 2 with different internal angles R, θ can be calculated, and the unfolded material size L of the whole bending part can be calculated. The formula can also be used to calculate the K and Y values of this kind of plate by bending the plate with known length, which can be used for the calculation of similar plates.

07 Closing remarks

In the production and processing of sheet metal bending, we can not only use the experience summary method to quickly calculate the common right angle bending unfolded material size, but also use the three-dimensional software to accurately calculate the unfolded material size of different R and θ bending through the formula. The K and Y values of unknown materials can be calculated flexibly by software and formula. It ensures that the sheet metal bending process, like other processing processes, can be accurately designed and processed.